条件概率讲解（如何理解条件概率？）

在大学学习概率中的条件概率时，其实有一种时而糊涂，时而清醒的感觉，说白了，还是没有真正的明白条件概率的意义，也没有真正的明白学习它到底是为了什么，到今天，我才真正的明白，条件概率就是研究多个事件的相关性的。

我用自己切身的经历来讲述事件的相关性是什么意思。

1. 什么是事件的相关性？

“相关” 的……意思是 受过去事件影响的…现实生活中有很多事件是相关事件，这里说一个真实的相关的案例：

事件的相关性

我在创业的初期，有一个错误的认识，认为线上的销售要优于线下的销售，所以，我的主要的经历都在线上，参加各种活动，目的是增加线上的销售额，在烧烤店的初期，确实外卖比较火热，走量走得比较多，但是随着附近也逐渐开了很多家的烧烤店后，我的线上的销售额远远不如从前，这时，我发现不能再按照这样的思路走下去了，于是，我开始了调研，惊奇地发现，线上的销售额只是总销售额的30%，我才发现，我在开店的初期，就走错了一步棋，不应该把全部的经历都放在线上，应该重视线下的销售，所以，我开始对门店进行重新的装修，菜谱也从原来的一张纸，变成了一个突显本店特色菜的本，也提高了店内的服务质量，比如，上菜的速度，桌子的卫生等，经过一系列的动作后，店内的销售额也提升了上来，线上的销售额也提升了上来。

讲了这么多，其实就想说的是，线上和线下其实就是相关的事件，要权衡把握。

1. 什么是条件概率？

上一节中，所讲的事件的相关性，事实上就是一种条件概率，就是说，事件A（我开店卖烤串），在事件B（全部精力投放到线上）发生的条件下，所发生的概率，就是条件概率，下面，就举一个学习概率时，常常遇到的红篮球的实验：

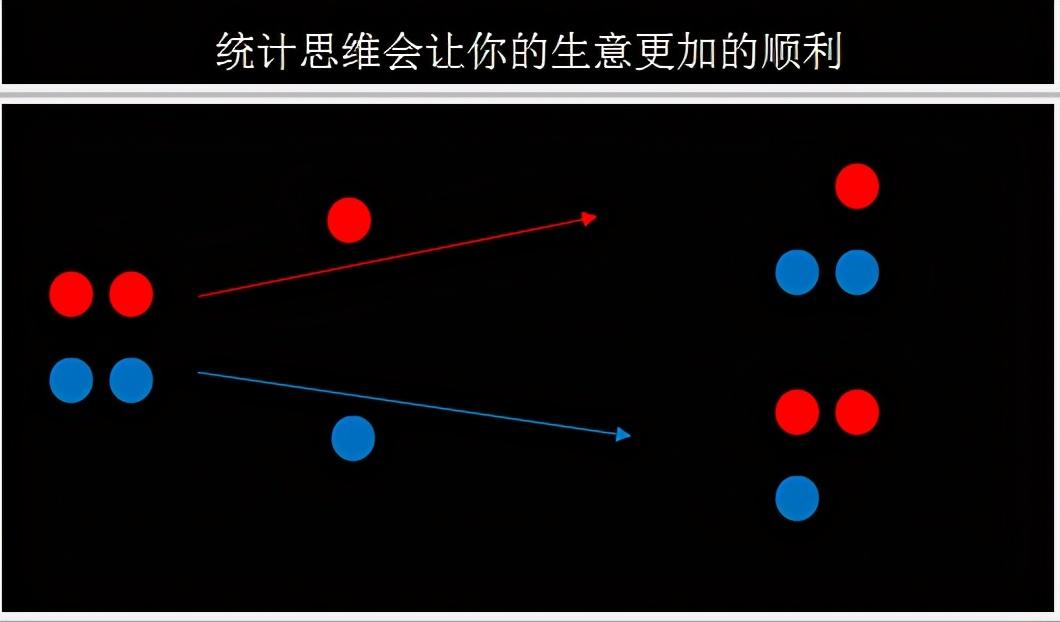
红篮球实验

现在口袋里有两个红色的球和两个蓝色的球，请问，随机从口袋里连续不放回的取两次，那么取到的两个球是蓝色球的概率是多少呢？

在计算概率之前，我们需要弄清楚，第1次拿球和第2次拿球是相关事件还是独立事情？

很显然，是相关的事件，因为第二次取球，受到第一次取球的影响，那么，现在算一算两次都取到蓝色球的概率是多少呢？

第一次取到蓝色球的概率，是1/2.

如果，第一次取到的是蓝色球，那么口袋里就剩下一个蓝色球和两个红球，那么第二次取到蓝色球的概率就是1/3，那么结果可想而知，结果留给你们来算哦。